In Euclidean Geometry, seven types of quadrilaterals are available, such as Square, Rectangle, Rhombus, Kite, Parallelogram, Trapezoid, Trapezium. The two-dimensional closed figure with two parallel sides is known as Trapezium. Some different categories of Trapezium are also available such as Scalene Trapezium, Isosceles Trapezium, Right Trapezium. But, the formula to calculate the area of Trapezium and the perimeter of a Trapezium is the same for all. This article will talk about the basic concepts of Trapezium, including its properties, applications, etc.
Shape of Trapezium
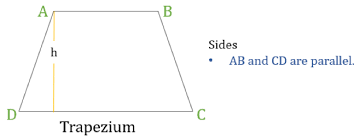
ABCD, Trapezium is shown below:
- AB and CD are two sides of the Trapezium, which are parallel to each other known as the base of the Trapezium.
- AD and BC are legs of Trapezium, and two non-parallel to each other.
For instance: In real lifelike windows, doors, tables, parks, etc.
Types of Trapezium
- Scalene Trapezium
- Isosceles Trapezium
- Right Trapezium
- Scalene Trapezium: Trapezium in which neither the angels nor the sides are equal is recognized as Scalene Trapezium.
- Isosceles Trapezium: Trapezium in which both legs are equal is recognized as Isosceles Trapezium.
- Right Trapezium: Trapezium in which a minimum of two right angles are present is recognized as Right Trapezium.
Basic properties of Trapezium
- The sum of all the angles of Trapezium, same as other quadrilaterals, is 3600.
- Two parallel sides are present in the Trapezium.
- Diagonals bisect each other.
- Apart from Isosceles Trapezium, in all Trapezium non-parallel sides are unequal.
- One pair of parallel sides exists in the Trapezium.
- It has four unequal sides.
- Mid-segment is also present in a Trapezium. The line parallel to the base that joins midpoints of non-parallel sides is known as mid-segment.
Mid-segment = (sum of two parallel sides)/2
Formula to calculate the area:
In a 2-dimensional plan, the area can be defined as the region covered by Trapezium. The area can be represented by symbol A. The measuring unit of the area of Trapezium is square units such as cm2, m2, etc.
Area of Trapezium = (1/2) × Distance between parallel sides × sum of parallel sides.
A = (1/2) h (AB+CD)
Perimeter:
The perimeter of the Trapezium is defined as the measurement of the outer edges of the Trapezium.
Perimeter (P) = AB+BC+CD+DA ie. Sum of all sides of Trapezium.
Example 1: A Trapezium with bases 20 cm and 32 cm. and with height 2 cm. Solve the area of a Trapezium with given information.
Solution: Given values are:
The bases are a = 20 cm; b = 32 cm.
The given height (h) = 2 cm.
The area of the Trapezium is, A = ½ h (a + b)
⇒ A = ½ (2)(20 + 32) = ½ (2)(52) = 52 cm2.
Example 2: If the perimeter of a Trapezium is 52 m and the sum of three sides is 45 m. using this information find the fourth side of the trapezium.
Solution: The formula to calculate perimeter is P = sum of all four sides of the Trapezium
And P is given = 52 m
The sum of three sides are given = 45 m
Now,
The fourth side of Trapezium = P – sum of three sides of the Trapezium
The fourth side = 52 – 45 = 7 m.
Various applications of Trapezium
- It has an extensive range of applications. It is used in physics, mathematics for solving a variety of problems.
- In construction work, it is used in finding the area of the trapezoidal roof.
- The formula can be used to find the area and perimeter of the Trapezium-shaped park yard.
For more clarity, use Cuemath which is an online learning platform for mathematics. A variety of questions and answers are present on this platform. Every concept related to Triangle, Rectangle, Square, Parallelograms, Trapezium is available here. Anyone can easily understand the concepts related to mathematics under the watchful guidance of expert teachers.